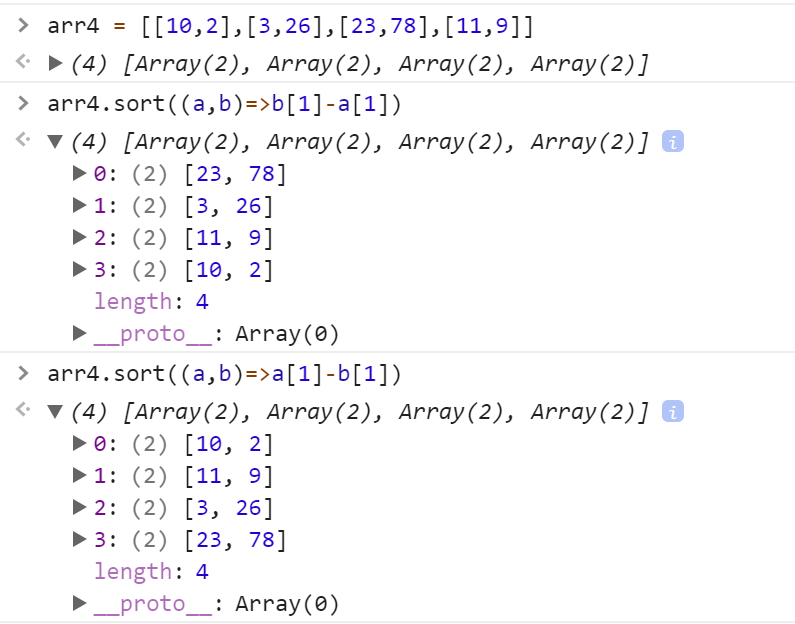
js内置函数排序
数组从小到大排序

字母从a-z、z-a排序

二维数组按照第二个元素排序
原生方法
- 冒泡排序
1 | // 冒泡排序: 比较两个相邻的项,如果第一个大于第二个则交换他们的位置,元素项向上移动至正确的顺序,就好像气泡往上冒一样 |
- 快速排序
1 | // 1) 首先,在数组中选择一个中间项作为主元 |
- 选择排序
1 | // 选择排序:大概思路是找到最小的放在第一位,找到第二小的放在第二位,以此类推 算法复杂度O(n^2) |
- 插入排序
1 | // 插入排序:每次排一个数组项,假设数组的第一项已经排序,接着,把第二项与第一项进行对比,第二项是该插入到第一项之前还是之后,第三项是该插入到第一项之前还是第一项之后还是第三项 |
- 归并排序
1 | // 归并排序:Mozilla Firefox 使用归并排序作为Array.prototype.sort的实现,而chrome使用快速排序的一个变体实现的,前面三种算法性能不好,但归并排序性能不错 算法复杂度O(nlog^n) |
- 堆排序
1 | //堆排序:堆排序把数组当中二叉树来排序而得名。 |
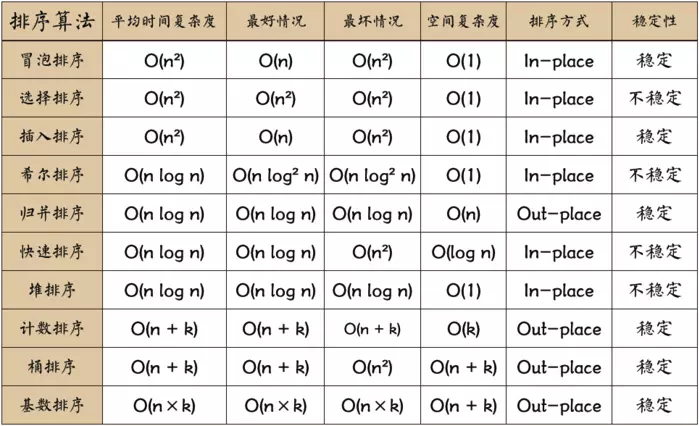
各种排序的复杂度比较